Automatic Optimization
CST Studio Suite Offers Automatic Optimization Routines for Electromagnetic Systems and Devices
Parmeterization and Optimization with CST Studio Suite
Parameterization of Simulation Models
CST Studio Suite models can be parameterized regarding their geometric dimensions or material properties. You can introduce parameters at any time, during the modeling process or retrospectively. Users can access their parameterization through the user interface to perform studies of the behavior of a device as its properties change.
Parameter Studies and Automatic Optimization
With a parameter study, users can find the optimum design parameters to achieve a given effect or fulfill a certain goal. They can also adapt material properties to fit material models to measured data.
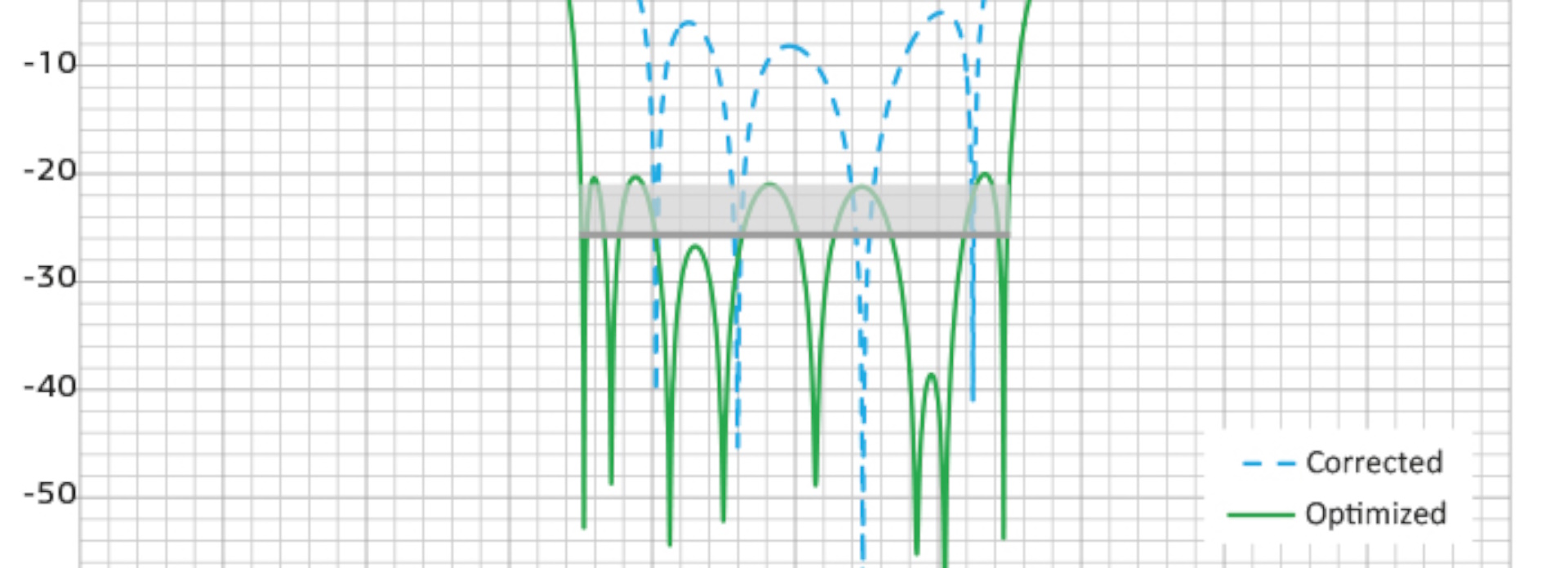
CST Studio Suite contains several automatic optimization algorithms, both local and global. Local optimizers provide fast convergence but risk converging to a local minimum rather than the overall best solution. On the other hand, global optimizers search the entire problem space but typically require more calculations.
Accelerating the Optimization Process
The time required for an optimization depends on the solution time for an individual electromagnetic simulation as well as on the number of iterations required to come to the optimum solution. High-performance computing techniques can be used to accelerate simulation and optimization for very complex systems, or problems with large numbers of variables.
The overall performance of global optimizers and independent parameter studies benefits from the ability to run individual sets in parallel. Distributed computing can greatly improve the performance for these applications.
CST Studio Suite Optimizers
The Covariance Matrix Adaptation Evolutionary Strategy (CMA-ES) is the most sophisticated of the global optimizers, and has relatively fast convergence for a global optimizer. With CMA-ES, the optimizer can “remember” previous iterations, which can help to improve the performance of the algorithm while avoiding local optimums.
Suitable for: General optimization, especially for complex problem domains
A powerful local optimizer, which builds a linear model on primary data in a "trust" region around the starting point. It uses the modeled solution as a new starting point until it converges to an accurate model of the data. The Trust Region Framework can take advantage of S-parameter sensitivity information to reduce the number of simulations needed and accelerate the optimization process. It is the most robust of the optimization algorithms.
Suitable for: General optimization, especially on models with sensitivity information
Using an evolutionary approach to optimization, the Genetic Algorithm generates points in the parameter space and then refines them through multiple generations, with random parameter mutation. By selecting the “fittest” sets of parameters at each generation, the algorithm converges to a global optimum.
Suitable for: Complex problem domains and models with many parameters
Another global optimizer, this algorithm treats points in parameter space as moving particles. At each iteration, the position of the particles changes according to, not only to the best known position of each particle, but also the best position of the entire swarm. Particle Swarm Optimization works well for models with many parameters.
Suitable for: Models with many parameters
This method is a local optimization technique which uses multiple points distributed across the parameter space to find the optimum. Nelder Mead Simplex Algorithm is less dependent on the starting point than most local optimizers.
Suitable for: Complex problem domains with relatively few parameters, systems without a good initial model
The interpolated Quasi-Newton optimizer is a fast local optimizer which uses interpolation to approximate the gradient of the parameter space. The Interpolated Quasi-Newton method has fast convergence.
Suitable for: Computationally demanding models
The Classic Powell optimizer is a simple, robust local optimizer for single-parameter problems. Although slower than the Interpolated Quasi-Newton, it can sometimes be more accurate.
Suitable for: Single-variable optimization
A specialized optimizer for printed circuit board (PCB) design, the Decap Optimizer calculates the most effective placement of decoupling capacitors using the Pareto front method. The optimizer helps to minimize either the number of capacitors needed or the total cost while still meeting the specified impedance curve.
Suitable for: PCB layout
Also Discover
Electromagnetic Field Simulation Software
CST Studio Suite Simulation Solvers for Electromagnetic Systems and Devices
CST Studio Suite Offers Graphical User Interface for Electromagnetic Systems and Devices
CST Studio Suite Provides an Environment that Simplifies the Management of Simulation Projects
CST Studio Suite Import and Data Exchange Options to Streamline Electromagnetic Design
Learn What SIMULIA Can Do for You
Speak with a SIMULIA expert to learn how our solutions enable seamless collaboration and sustainable innovation at organizations of every size.
Get Started
Courses and classes are available for students, academia, professionals and companies. Find the right SIMULIA training for you.
Get Help
Find information on software & hardware certification, software downloads, user documentation, support contact and services offering