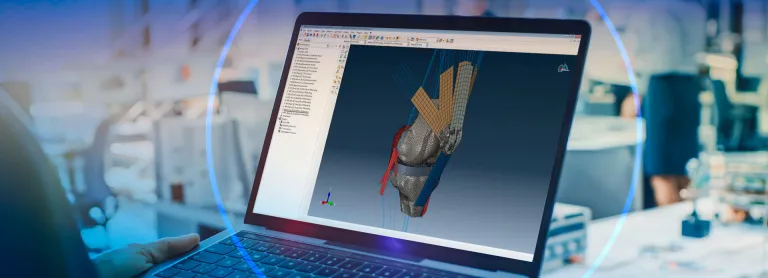
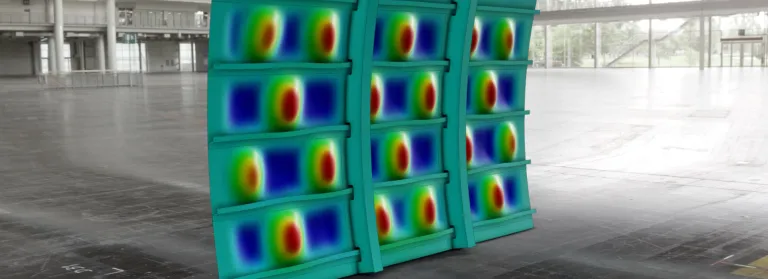
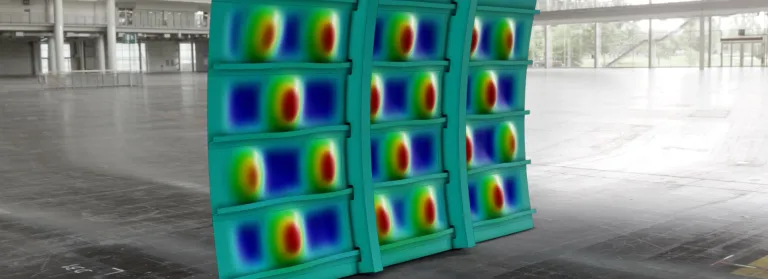
Abaqus Multiphysics
Complete Solutions for Realistic Simulation
Multiphysics Simulation & Analysis in Abaqus
The different physical disciplines such as structural mechanics, fluid dynamics, thermodynamics and electromagnetics are tightly connected because the interaction between multiple physical phenomena and the conversion of energy from one form to another is crucial to most industrial applications.
For example, to design efficient and reliable lithium-ion batteries, engineers must account not just for the electrochemical behavior but also for thermal runaway and fluid dynamics of the electrolyte and structural bending and swelling. Even during manufacturing, multiphysical effects must be controlled, whether the plastic flow in injection molding or moisture build-up during electronic assembly.
The Abaqus Unified FEA product suite has significant capabilities for solving multiphysics problems. These capabilities, developed over many years and fully integrated as core Abaqus functionality, have been used extensively for many engineering applications on products and engineering projects today.
Multiphysics technology has been a part of Abaqus from the beginning. Starting with Abaqus V2 (in 1979), Abaqus/Aqua simulates hydrodynamic wave loading on flexible structures for offshore pipelines. Through the years, additional multiphysics capabilities have been added, such as fluid, thermal, electrical couplings, and many others listed below.
Creating a Multiphysics Simulation Flow in Abaqus
To address these challenging applications, Abaqus offers a range of multiphysics simulation capabilities, including sequential results mapping, fully-coupled solution procedures, and co-simulation:
- Sequential results mapping - The external field capability in Abaqus provides a general framework for mapping results from an upstream simulation onto an Abaqus simulation. Examples include mapping temperature from an upstream heat transfer simulation and mapping pressure from an upstream fluid dynamics simulation.
- Fully-coupled simulation - When the one-way coupling is insufficient, Abaqus offers fully coupled solution procedures, including thermal stress, thermal-electrochemical-structural, acoustic-structural, and fluid flow through porous media.
- Co-simulation - An open co-simulation framework provides the ability to connect Abaqus with external solvers.
The advantage of Abaqus Multiphysics is the ease with which the Abaqus structural FEA user can solve Multiphysics problems. From the same model, same element library, same material data, and same load history, an Abaqus structural FEA model can easily be extended to include additional physics interaction.
Multiphysics Capabilities inside Abaqus
- Coupled Eulerian-Lagrangian Simulation
- Hydrostatic-Fluid-Mechanical Simulation
- Piezoelectric-Mechanical Simulation
- Structural-Acoustic Simulation
Coupled Eulerian-Lagrangian Simulation
The Coupled Eulerian-Lagrangian (CEL) approach in Abaqus allows engineers and scientists to simulate problems where the interaction between structures and fluids is important. This capability does not rely on coupling multiple software products but solves the fluid-structure interaction (FSI) simultaneously within Abaqus.
Hydrostatic-Fluid-Mechanical Simulation
The Hydrostatic-Fluid-Mechanical Multiphysics capability allows the user to include the effects of fully enclosed gas- or liquid-filled cavities in their model. This is useful for simulating balloons, air bags, seat cushions, athletic shoes, partially filled tanks and other containers, air springs, IV bags, and many other applications that require consideration of the pressure-volume relationship of the enclosure and the energy inside the enclosed fluid.
Piezoelectric-Mechanical Simulation
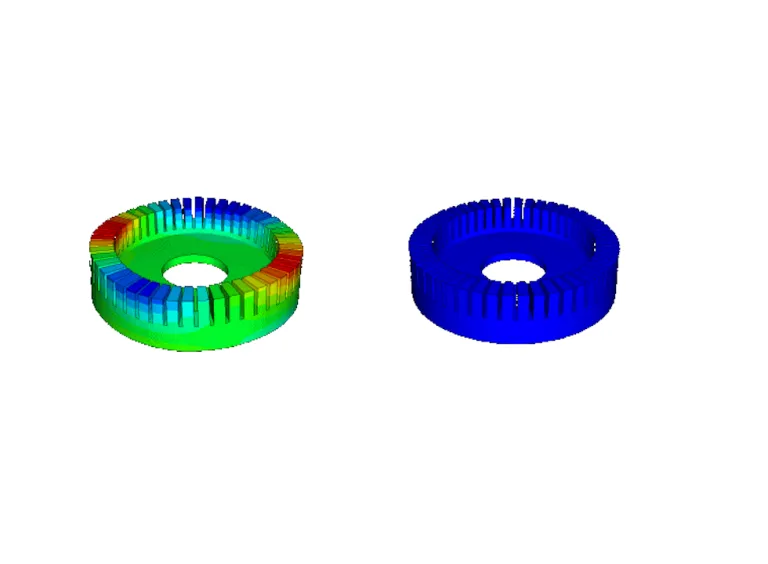
Abaqus contains a complete two-way electrostatic Piezoelectric-Mechanical simulation capability, allowing electric flow to cause strain in the material (and shape change) and stress to cause electric potential change.
Structural-Acoustic Simulation
Structural-acoustic interaction covers diverse application areas, including noise transmission, radiation, acoustic attenuation or amplification. Abaqus integrates noise simulation within the finite element solver, allowing fully coupled structural acoustic simulations to be performed within familiar Abaqus workflows.
- Thermal-Electric Simulation
- Thermal-Mechanical Simulation
- Thermal-Fluid-Mechanical Simulation
- Structural-Pore Pressure Simulation
Thermal-Electric Simulation
Current flow generates heating, heating changes resistivity, and resistivity change alters current flow. This type of simulation is useful in sensitive electronic devices such as fuses, links, electrical traces, and lightbulb filaments.
Thermal-Mechanical Simulation
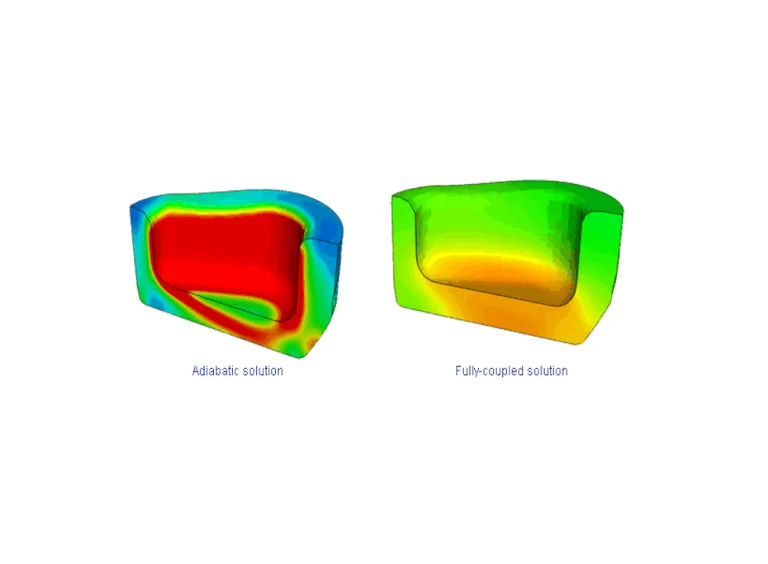
Thermal-mechanical interaction ranges from simple thermal stress (one-way coupling from thermal simulation to stress analysis) to more complex friction-driven heat transfer (in which frictional sliding generates heat as in brake systems) to fully coupled temperature-displacement simulation (in which motion affects heat transfer and heat transfer affects motion).
Thermal-Fluid-Mechanical Simulation
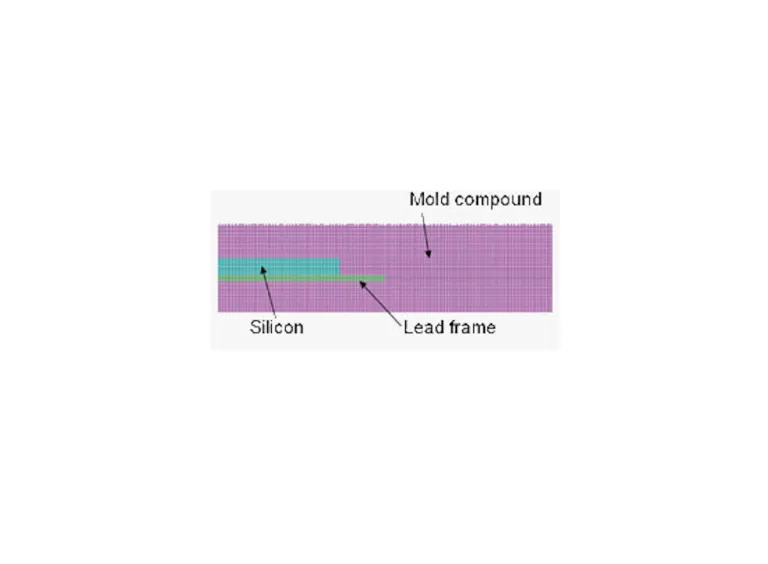
In many industrial processes, the combined effects of moisture and heat on product performance or behavior during assembly can be critical. By simultaneously considering the detailed behavior of the product under realistic operating conditions, designers and engineers can determine the ideal design or manufacturing process for a given performance goal.
Structural-Pore Pressure Simulation
The influence of water on the behavior of soils under load is extremely complex, and a sophisticated coupled approach is required to provide simulation results, which can help provide confidence in design decisions.
Start Your Journey
Explore the technological advancements, innovative methodologies, and evolving industry demands reshaping the world of Multiphysics Technology. Stay a step ahead with SIMULIA. Discover Abaqus Multiphysics now.
FAQs About Multiphysics Simulation
Multiphysics simulation is a computational technique that solves complex problems involving multiple physical processes or phenomena. It offers several benefits that significantly enhance complex systems' design, analysis, and optimization.
- Comprehensive Insight: It enables analyzing real-world systems and phenomena where multiple physical factors interact, such as thermal effects on structural integrity, providing a more accurate and holistic understanding of system behaviors.
- Cost Reduction: Predicting and optimizing the performance of designs or processes before physical prototypes are built can significantly reduce the time and money spent on experimental testing.
- Innovation and Optimization: Facilitates the exploration of a wider design space and assesses more variables and their interactions than traditional single-physics simulations, leading to innovative solutions and optimized designs that wouldn’t be possible otherwise.
- Risk Mitigation: Helps identify potential design issues and failure points by simulating various operating conditions and extreme scenarios, thereby enhancing safety and reliability.
- Faster Time-to-Market: Accelerates the development process of products by enabling rapid iterations of the design based on simulation feedback, reducing the overall time from concept to market.
Multiphysics simulation software is a computational tool that simulates and analyzes the interactions between different physical phenomena—such as thermal, mechanical, electrical, and fluid dynamics—within a single framework. This allows for the comprehensive study and optimization of complex systems that involve multiple interacting physical processes.
Also Discover
Learn What SIMULIA Can Do for You
Speak with a SIMULIA expert to learn how our solutions enable seamless collaboration and sustainable innovation at organizations of every size.
Get Started
Courses and classes are available for students, academia, professionals and companies. Find the right SIMULIA training for you.
Get Help
Find information on software & hardware certification, software downloads, user documentation, support contact and services offering